Extras: Type 0 Systems Examples

Let's say that we have a unity-feedback system as shown below

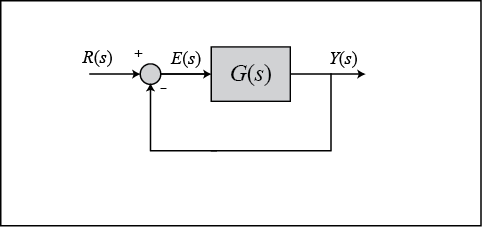
where G(s) is the following.

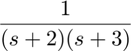
(1) $\frac{1}{(s+2)(s+3)}$

Let's look at the closed-loop response for this system when we use different inputs.

Step Input

s = tf('s');
G = 1/((s+2)*(s+3));
sys_cl = feedback(G,1);
[y,t] = step(sys_cl);
u = ones(size(t));
plot(t,y,'y',t,u,'m')
axis([0,2.9,0,1.1])
xlabel('Time(secs)')
ylabel('Amplitude')
title('Input-purple, Output-yellow')

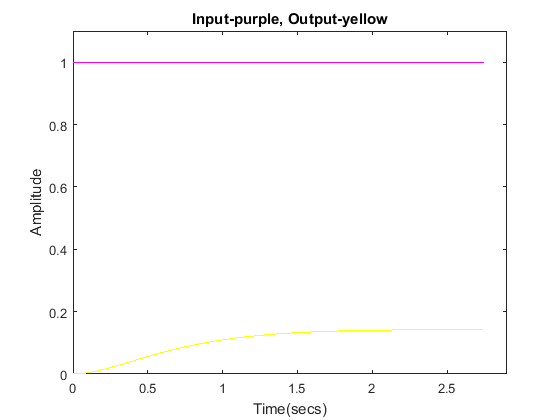
Our steady-state error is a constant.

Ramp Input

s = tf('s');
G = 1/((s+2)*(s+3));
sys_cl = feedback(G,1);
t = 0:0.1:200;
u = t;
[y,t,x] = lsim(sys_cl,u,t);
plot(t,y,'y',t,u,'m')
xlabel('Time(secs)')
ylabel('Amplitude')
title('Input-purple, Output-yellow')

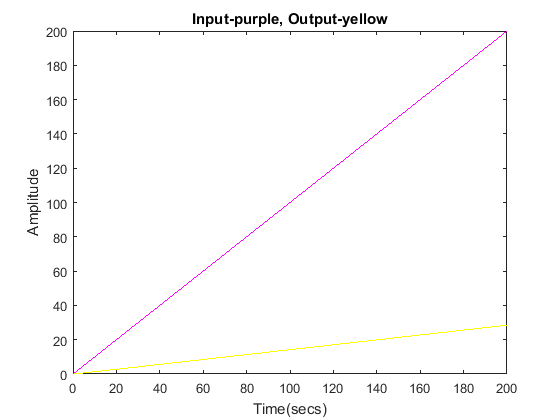
Our steady-state error is infinite (the error grows unbounded as time increases toward infinity).

Parabolic Input

s = tf('s');
G = 1/((s+2)*(s+3));
sys_cl = feedback(G,1);
t = 0:0.1:200;
u = 0.5*t.*t;
[y,t,x] = lsim(sys_cl,u,t);
plot(t,y,'y',t,u,'m')
xlabel('Time(secs)')
ylabel('Amplitude')
title('Input-purple, Output-yellow')

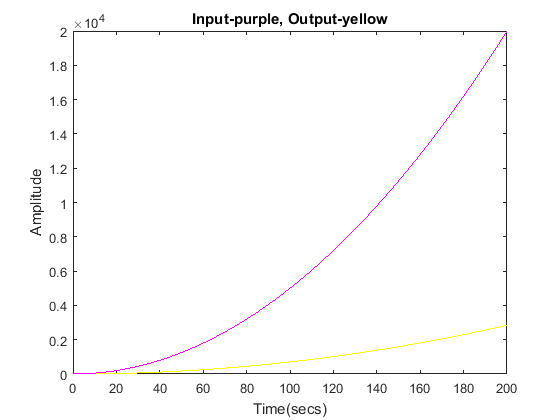
Our steady-state error is infinite (the error grows unbounded as time increases toward infinity).